

Sometimes we may want to use one or more sets to create a new set in an interesting way. We may want to have a formal way to "put two sets together" or to "find all the elements that two sets have in common." This desire to find a way to make a new set from one or more old sets motivates us to come up with operations on sets.
Formally we can write: A∪B = {x| x∈A or x∈B}. This just means that any element of A∪B must be an element of the set A OR of the set B (or both).
(Remember, out loud we would say, “the set of all x’s such that x is an element of A or x is an element of B (or both).”
Be careful not to confuse the symbol for union ∪ with the uppercase letter U, which we use to represent the universal set! Notice that the union symbol does NOT have any lines at the top; the union symbol is composed of a single curved line.
To see what a union looks like on a Venn diagram, we draw our two sets A and B on a Venn diagram as below:
An empty Venn diagram with ovals indicating where the sets A and B could go:

If we want to draw a diagram of A∪B, we first need to draw a diagram of A and a diagram of B, and then we have to determine how to take the union of the two diagrams:
A
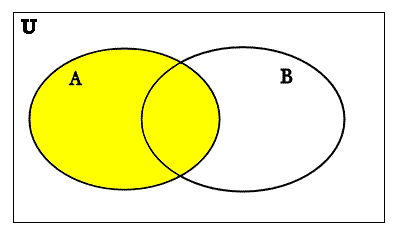
In this diagram of A, the shaded yellow part indicates the set A.
B
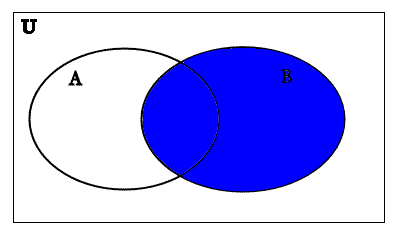
In this diagram of B, the shaded blue part indicates the set B.
Now we put both of these diagrams together, putting both the yellow shading and the blue shading onto the basic venn diagram:
A in yellow; B in blue

In this diagram, A is indicated by yellow shading, B is indicated by blue shading, and the green part appears where both yellow and blue have been shaded. So the yellow part now indicates only that part of A that is not also in B. The blue part now indicates the part of B which is not in A. And the green part indicates that part of A and that part of B which both sets have in common.
We recall that taking the union means that we would take all elements that are either in A or in B or in both; so this means, that to create the venn diagram of the union of two sets, we look at the diagram where the two sets have been shaded in together, and for our final diagram, we shade in any part that was shaded yellow, or blue, or green in the previous diagram - in other words, the final diagram contains any shading that was previously of any color, but the final diagram uses only one color to indicate the new set A∪B.
So now we shade in A∪B in red on a new venn diagram:
A∪B

Notice that our final venn diagram only includes ONE color; if we use more than one color on a venn diagram, it is unclear which color(s) indicate the set which is labeled at the top of the diagram
Now let’s look at a few specific sets and practice taking the union of them.
Let A={1.1, 1.2, 1.3} and B={1.2, 1.4, 1.6}. If we take every element of A and every element of B and put them all together, we get A∪B={1.1, 1.2, 1.3, 1.4, 1.6}.
Let A={0,1,2,3} and let B={5,6,7,8,9,10}. Then if we take every element of A and every element of B and put them all together, we get A∪B={0,1,2,3,5,6,7,8,9,10}.
Notice that when we take the union of two sets, we do not repeat elements that occur in both sets; if an element appears in both sets, we only write it once in the union. This is because with sets, repetition of elements does not change the set.
Formally we can write: A∩B = {x| x∈A and x∈B}. This just means that if an element is in the set A∩B, then it is both an element of the set A AND an element of the set B.
(Remember, out loud we would say, “the set of all x’s such that x is an element of A and x is an element of B.”
To see what an intersection looks like on a Venn diagram, we draw our two sets A and B on a Venn diagram as below:
An empty Venn diagram with ovals indicating where the sets A and B could go:

If we want to draw a diagram of A∩B, we first need to draw a diagram of A and a diagram of B, and then we have to determine how to take the intersection of the two diagrams:
A

In this diagram of A, the shaded yellow part indicates the set A.
B

In this diagram of B, the shaded blue part indicates the set B.
Now we put both of these diagrams together, putting both the yellow shading and the blue shading onto the basic venn diagram:
A in yellow; B in blue

In this diagram, A is indicated by yellow shading, B is indicated by blue shading, and the green part appears where both yellow and blue have been shaded. So the yellow part now indicates only that part of A that is not also in B. The blue part now indicates the part of B which is not in A. And the green part indicates that part of A and that part of B which both sets have in common.
We recall that taking the intersection means that we would take only elements that are both in A and in B; so this means, that to create the venn diagram of the intersection of two sets, we look at the diagram where the two sets have been shaded in together, and for our final diagram, we shade in only the parts that were shaded both yellow and blue in the previous diagram - in other words, the final diagram contains only the green shading; again, the final diagram uses only one color to indicate the new set A∩B.
So now we shade in A∩B in red on a new venn diagram:
A∩B

Let’s look at a few sets and practice taking the intersection of them.
Let A={1.1, 1.2, 1.3} and B={1.2, 1.4, 1.6}. If we take only the elements that are in both A and B at the same time and put them all together, we get A∩B={1.2}.
Let A={10, 20, 30, 40} and B={10, 15, 20, 25, 30}. If we take only the elements that are in both A and B at the same time and put them all together, we get A∩B={10, 20, 30}.
Let A={0,1,2,3,4} and let B={5,6,7,8,9,10}. Then if we take only the elements that are in both A and B at the same time and put them all together, we get A∩B= Ø, because there are NO elements in both A and B at the same time. A and B don’t overlap or intersect at all, so their intersection is the null set, or empty set. We have a special name for sets like these:
When the intersection of two sets is empty, we say that the two sets are DISJOINT.
If we drew two disjoint sets on a Venn diagram, they would look like this:

Formally we can write: A′ = {x| x∈U but x∉A}. This just means that in order for an element to be in the set A′, it canNOT be an element of the set A.
(Remember, out loud we would say, “the set of all x’s such that x is an element of the universal set but x is NOT an element of A.”)
To see what a complement looks like on a Venn diagram, we begin with an empty Venn diagram as below. We will do this problem 2 ways: on the left, we see a venn diagram where only the set A is indicated. This is the simplest way to draw a picture of the set A. On the right, we see a venn diagram where both the sets A and B are indicated. This is unnecessary, but it is good to see an example where we take the complement of one set when another set is present, because we will often need to do this in more complicated examples which follow in the next section.
An empty Venn diagram with ovals indicating where the set A could go: |
An empty Venn diagram with only one oval indicating where the sets A and B could go: |
 |
 |
If we want to draw a diagram of A′, we first need to draw a diagram of A, and then we have to determine how to take the complement of that diagram:
A |
A |
 |
 |
In these two possible diagrams of A, the shaded yellow part indicates the set A.
We recall that taking the complement means that we would take only elements that are not in A but which are still in the universal set; so this means, that to create the venn diagram of the complement of a set, we look at the diagram where the set has been shaded in, and for our final diagram, we shade in only the parts that were not shaded in the previous diagram - in other words, the final diagram contains only the white areas.
So we shade in A′ in blue like this:
A′ |
A′ |
 |
 |
Both of these diagrams represent A′; the first diagram shows A′ in a diagram that only indicates A, while the second diagram shows A′ in a diagram where the set B is also present. Notice, however, that the presence of B does not affect any of the choices of where to shade in A or A′; B is simply there to remind us that another set also exists which is called B, and which is not relevant to the current task of finding the complement of A. If you ignore the oval indicating where the set B would go, the two diagrams look exactly the same.
For another example, if instead we wanted to find B′ on the empty venn diagram which looks like this:
An empty Venn diagram with ovals indicating where the sets A and B could go:

We would first shade in B in green:
B
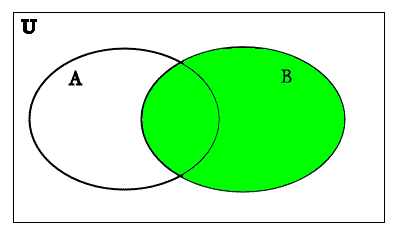
Then again we recall that taking the complement means that we would take only elements that are not in B but which are still in the universal set; so this means, that to create the venn diagram of the complement of a set, we look at the diagram where the set has been shaded in, and for our final diagram, we shade in only the parts that were not shaded in the previous diagram - in other words, the final diagram contains only the white areas.
So we shade in B ′ in red like this:
B′

Let’s look at a few sets and practice taking the complement of them.
Let U={1,2,3,4,5} and A={1,3,5}. If we take every element of U that is NOT in A and put them into a single set, we get A′={2,4}.
Let U={3.5, 4.5, 5.5} and let A={3.5, 4.5, 5.5}. If we take every element of U that is NOT in A and put them into a single set, we get A′= Ø, because there are no elements that are not in A, but which are in the universal set - all the elements of A are also in the universal set.
Let U={1,2,3,…} and let A={1,2,3,4,5}. If we take every element of U that is NOT in A and put them into a single set, we get A′={6,7,8,…}.
Let U=Z and let A= Ø. If we take every element of U that is NOT in A and put them into a single set, we get A′=U=Z. Because there is nothing in A, the complement of A is the universal set itself. Because A has no elements, there isn't a single element of the universal set which is not in A. (Remember that a set put together with its complement should give you U.)
Formally we can write: A-B = {x| x∈A but x∉B}. This just means that any element of A-B must be an element of A and cannot be an element of B.
(Remember, out loud we would say, “the set of all x’s such that x is an element of A but x is NOT an element of B.”
Notice that the complement of A, A′ is the same thing as U-A.
To see what a difference looks like on a Venn diagram, we draw our two sets A and B on a Venn diagram as below:
An empty Venn diagram with ovals indicating where the sets A and B could go:

If we want to draw a diagram of A-B, we first need to draw a diagram of A and a diagram of B, and then we have to determine how to take the difference of the two diagrams:
A

In this diagram of A, the shaded yellow part indicates the set A.
B

In this diagram of B, the shaded blue part indicates the set B.
Now we put both of these diagrams together, putting both the yellow shading and the blue shading onto the basic venn diagram:
A in yellow; B in blue

In this diagram, A is indicated by yellow shading, B is indicated by blue shading, and the green part appears where both yellow and blue have been shaded. So the yellow part now indicates only that part of A that is not also in B. The blue part now indicates the part of B which is not in A. And the green part indicates that part of A and that part of B which both sets have in common.
We recall that taking the difference means that we would take all elements that are in A and remove any elements that are also in B; so this means, that to create the venn diagram of the difference of two sets, we look at the diagram where the two sets have been shaded in together, and for our final diagram, we shade in any part that was shaded yellow but not blue in the previous diagram - in other words, the final diagram contains only the shading that appears yellow, not green or blue, and the final diagram uses only one color to indicate the new set A-B.
So now we shade in A-B in red on a new venn diagram:
A-B

Notice that our final venn diagram only includes ONE color; if we use more than one color on a venn diagram, it is unclear which color(s) indicate the set which is labeled at the top of the diagram
To see in fact that A-B does not in general equal B-A, we can draw a venn diagram of B-A and compare it to the one above of A-B.
If we want to draw a diagram of B-A, we first need to draw a diagram of B and a diagram of A, and then we have to determine how to take the difference of the two diagrams:
B

In this diagram of B, the shaded blue part indicates the set B.
A

In this diagram of A, the shaded yellow part indicates the set A.
Now we put both of these diagrams together, putting both the yellow shading and the blue shading onto the basic venn diagram:
A in yellow; B in blue

In this diagram, A is indicated by yellow shading, B is indicated by blue shading, and the green part appears where both yellow and blue have been shaded. So the yellow part now indicates only that part of A that is not also in B. The blue part now indicates the part of B which is not in A. And the green part indicates that part of A and that part of B which both sets have in common.
We recall that taking the difference means that we would take all elements that are in B and remove any elements that are also in A; so this means, that to create the venn diagram of the difference of two sets, we look at the diagram where the two sets have been shaded in together, and for our final diagram, we shade in any part that was shaded blue but not yellow in the previous diagram - in other words, the final diagram contains only the shading that appears blue, not green or yellow, and the final diagram uses only one color to indicate the new set B-A.
So now we shade in B-A in blue on a new venn diagram:
B-A

We can now clearly see that A-B does not in general equal B-A, because their two venn diagrams are not the same:
A-B

B-A

Notice that we can tell that A-B does not equal B-A no matter what the sets A and B are because venn diagrams depict all possible sets A and B, and the only way that these two pictures could be the same is if there is actually nothing in A or B, so that any place that is shaded in the venn diagram for A-B and for B-A is empty.
Let’s look at a few sets and practice taking the complement of them.
Let A={1,2,3,4,5} and B={1,3,5}. If we take every element of A that is NOT in B and put them in a new set, we get A-B={2,4}.
Let A={3.5, 4.5, 5.5} and let B={3.5, 4.5, 5.5}. If we take every element of A that is NOT in B and put them in a new set, we get A-B= Ø, because all the elements of A are also in B, so they will not be in the difference - remember that the difference never contains any elements belonging to the second set.
Let A={1,2,3,…} and let B={1,2,3,4,5}. If we take every element of A that is NOT in B and put them in a new set, we get A-B={6,7,8,…}.
Let A=Z and let B= Ø. If we take every element of A that is NOT in B and put them in a new set, we get A-B=U=Z. Because there is nothing in B, the difference between A and B is A itself.
Notice that if we take the union of B and A-B we will get A.
Do you notice the similarities between the complement and the difference between two sets? We could redefine A′ as U-A.
Be careful when taking the difference of two sets - the difference should NEVER contain any elements which belong to the SECOND set! The difference should basically be the FIRST set with any elements that belong also to the SECOND set REMOVED.
A very common mistake students often make when computing A-B is to include any elements of A which are not in B and any elements of B which are not in A - this is incorrect! There should be NO elements of B in A-B! For example, if A={b,i,r,d} and B={s,h,i,r,t}, notice that A-B DOES NOT EQUAL {b,d,h,s,t}, because this set includes h, s, and t, which are all elements of B!